Description
Markets are like twigs. When fresh and green, they're pliable. They bend but don't break easily. As they age and dry out they become more brittle and more susceptible to breakage when force is applied to them. When the twig breaks, a new green shoot is formed and the cycle repeats. This indicator anticipates when the twig is about to snap.
torsion |ˈtɔːʃ(ə)n|
noun [ mass noun ]
the action of twisting or the state of being twisted, especially of one end of an object relative to the other. In mathematics the extent to which a curve departs from being planar.
This indicator combines two independently adjustable polynomial regression channel and centre of gravity indicators (see. Mostafa Belkhayate), and a novel torsion indicator, which visualises the degree of stress between current market momentum and recent historical trend & volatility action. Put another way, it could be said to be describing the market turning moment relative to the market trajectory (market torsion).
The output of the torsion indicator is displayed on the chart as the pink line (TAU). This indicator also includes, optionally, a pair of Hull Moving Averages, a Triangular Moving Average and Fractal Chaos Bands. Torsion is only calculated on polynomial regression channels of the second degree or greater. A well tuned Torsion Indicator can anticipate trend reversals with remarkable accuracy, as it crosses through the price action or one of the regression channel boundaries. Higher polynomial degrees increase torsion sensitivity, as do longer torsionPeriod values (which are normally effective in the 5-50 period range).
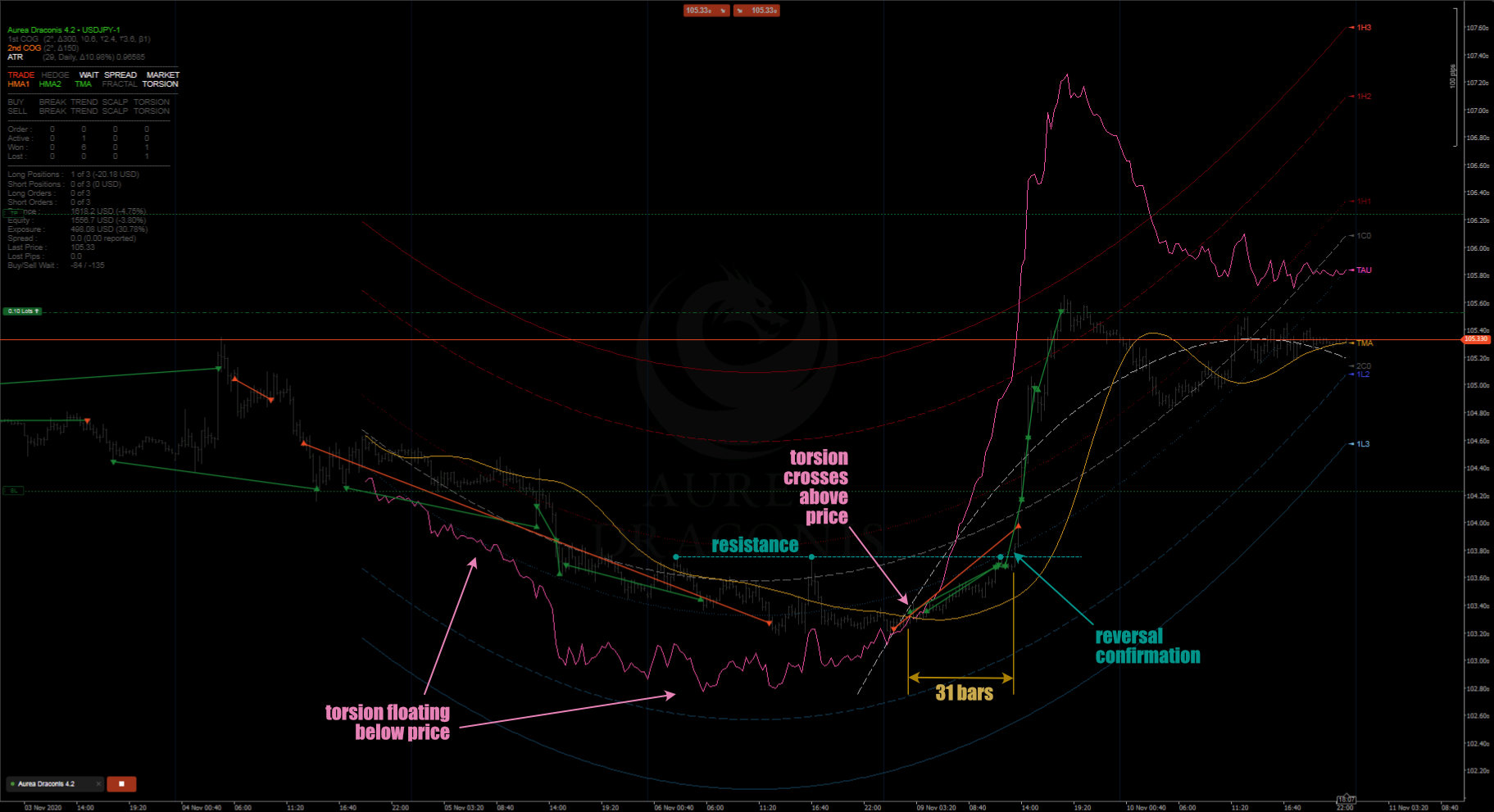
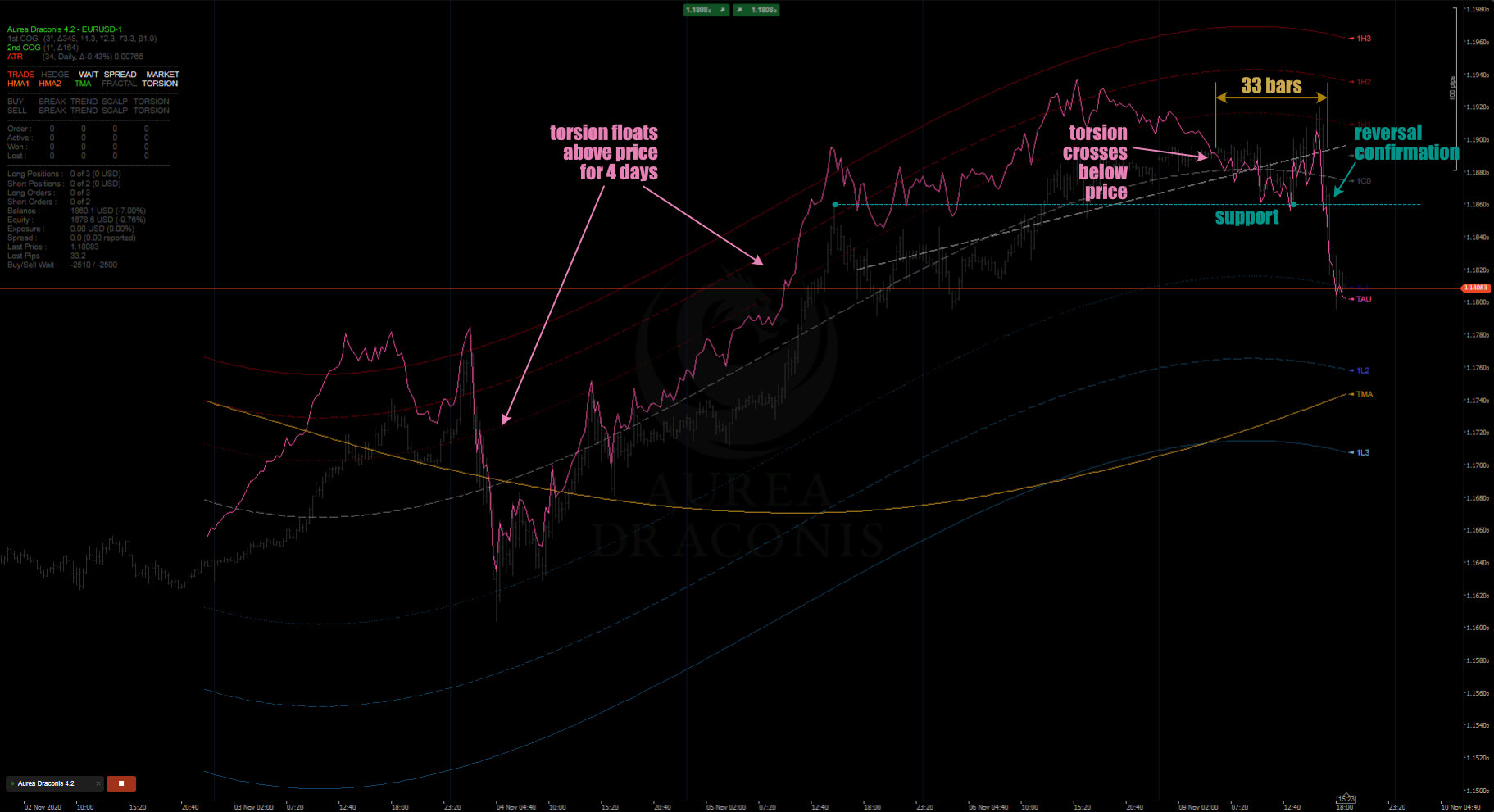
The Torsion Indicator is the foundation of the Aurea Draconis cBot. A free demo of the cBot and backtest results using this indicator are available here. Trades, targets and stop positions can be triggered in the Aurea Draconis cBot as TAU passes though the price action, the centreline (1C0), or through any of the regression bands (1H3, 1H2, 1H1, 1L1, 1L2, 1L3) in either direction. As such, torsion generated signals can be utilised for swing trading, trend following, breakout, scalping and hedging strategies.
cBot Free Demo : https://draconis.trade/product/aurea-draconis-demo/
cBot Live Version : https://draconis.trade/purchase/
Timelapse Backtest : https://youtu.be/MUUcYGRMhOA
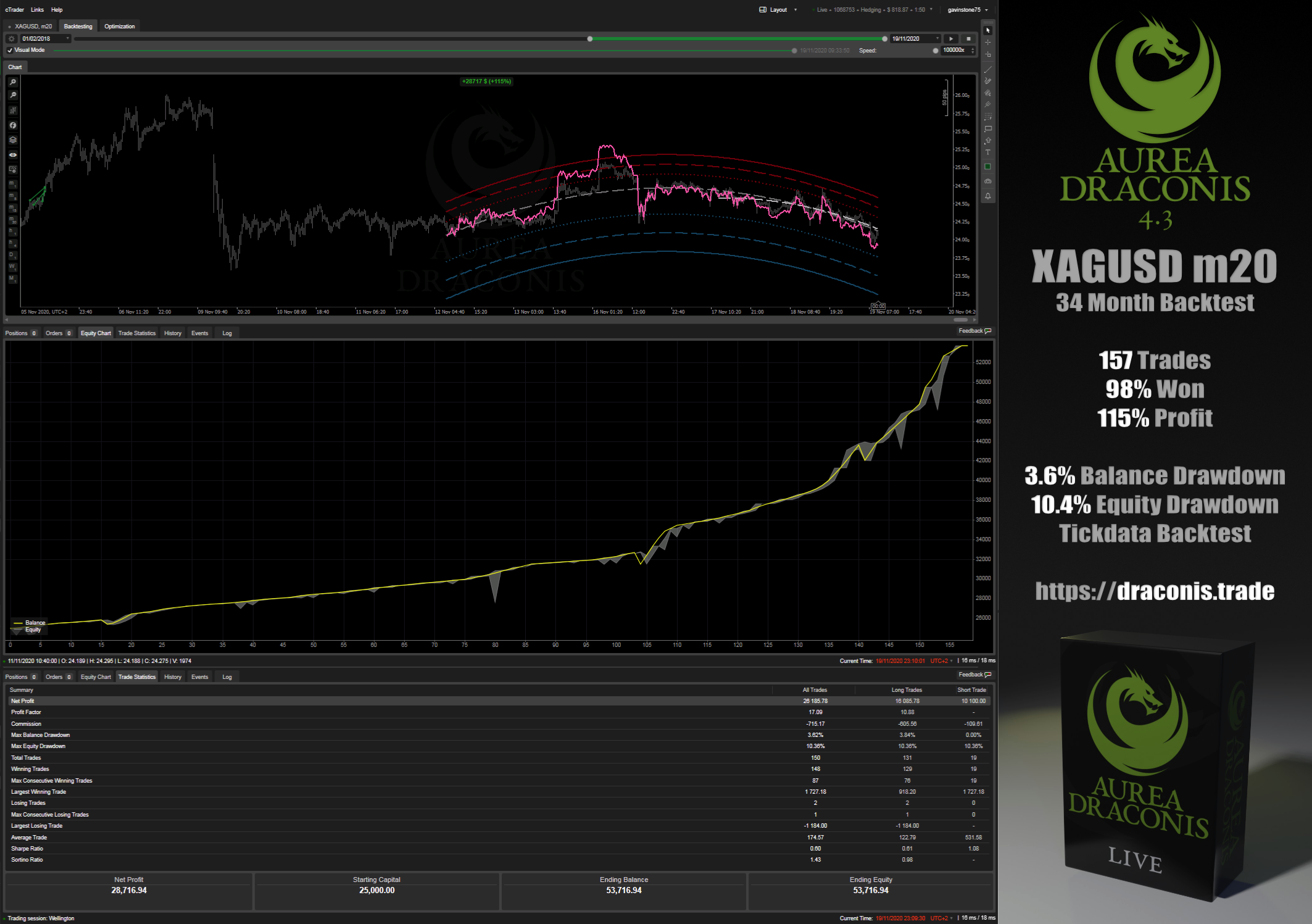
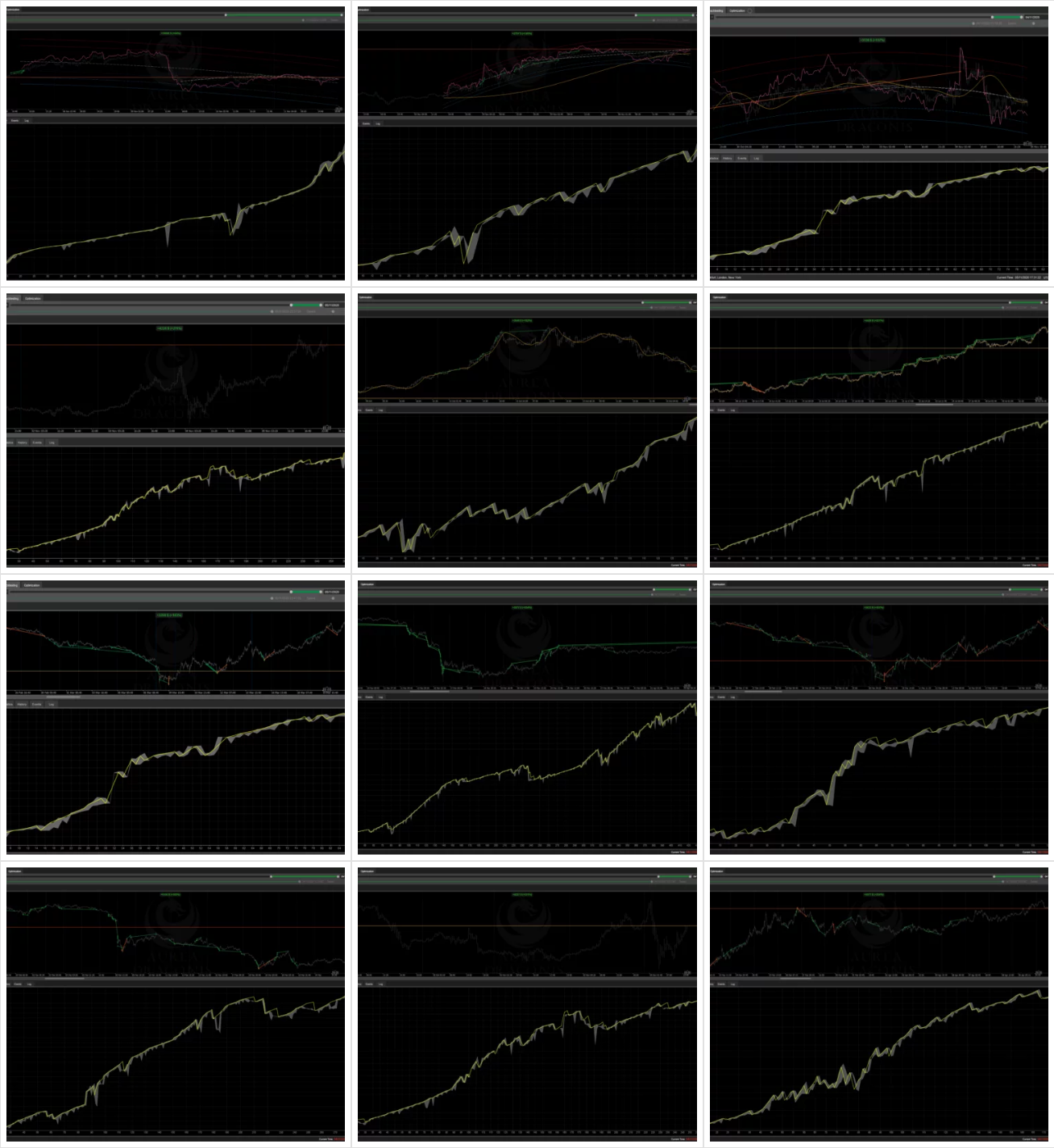
Some 1 and 2 year backtests run using this indicator and the Aurea Draconis cBot (full size images available here) :
CHANGE LOG
Version 4.3 (2020-11-11)
- Split the upper/lower band scaling into two independent parameters, longScale and shortScale.
// Aurea Draconis Torsion Indicator 4.3
// Released 2020-11-11
// Created by Craig Stone
using System;
using cAlgo.API;
using cAlgo.API.Internals;
using cAlgo.API.Indicators;
namespace cAlgo.Indicators
{
[Indicator(IsOverlay = true)]
public class AureaDraconisTorsion : Indicator
{
[Parameter(DefaultValue = 300)]
public int cog1Period { get; set; }
[Parameter(DefaultValue = 2, MinValue = 1, MaxValue = 4)]
public int cog1Degree { get; set; }
[Parameter(DefaultValue = 150, MinValue = 0)]
public int cog2Period { get; set; }
[Parameter(DefaultValue = 2, MinValue = 0, MaxValue = 4)]
public int cog2Degree { get; set; }
[Parameter(DefaultValue = 1.4)]
public double cogBand1 { get; set; }
[Parameter(DefaultValue = 2.4)]
public double cogBand2 { get; set; }
[Parameter(DefaultValue = 3.4)]
public double cogBand3 { get; set; }
[Parameter(DefaultValue = 1.0, MinValue = 0.1, MaxValue = 2.0)]
public double longScale { get; set; }
[Parameter(DefaultValue = 1.0, MinValue = 0.1, MaxValue = 2.0)]
public double shortScale { get; set; }
[Parameter(DefaultValue = 0, MinValue = 0)]
public int torsionPeriod { get; set; }
[Parameter(DefaultValue = 0, MinValue = 0)]
public int hma1Period { get; set; }
[Parameter(DefaultValue = 0, MinValue = 0)]
public int hma2Period { get; set; }
[Parameter(DefaultValue = 0, MinValue = 0)]
public int tmaPeriod { get; set; }
[Parameter(DefaultValue = false)]
public bool fractalFilter { get; set; }
[Parameter("Source")]
public DataSeries Source { get; set; }
[Output("C1H3", LineColor = "#FF800001", LineStyle = LineStyle.Solid)]
public IndicatorDataSeries c1h3 { get; set; }
[Output("C1H2", LineColor = "#FF800001", LineStyle = LineStyle.Lines)]
public IndicatorDataSeries c1h2 { get; set; }
[Output("C1H1", LineColor = "#FF800001", LineStyle = LineStyle.Dots)]
public IndicatorDataSeries c1h1 { get; set; }
[Output("COG1", LineColor = "Gray", LineStyle = LineStyle.Lines)]
public IndicatorDataSeries cog1 { get; set; }
[Output("C1L1", LineColor = "#FF025776", LineStyle = LineStyle.Dots)]
public IndicatorDataSeries c1l1 { get; set; }
[Output("C1L2", LineColor = "#FF025776", LineStyle = LineStyle.Lines)]
public IndicatorDataSeries c1l2 { get; set; }
[Output("C1L3", LineColor = "#FF025776", LineStyle = LineStyle.Solid)]
public IndicatorDataSeries c1l3 { get; set; }
[Output("COG2", LineColor = "Silver", LineStyle = LineStyle.Lines)]
public IndicatorDataSeries cog2 { get; set; }
[Output("TAU", LineColor = "HotPink", LineStyle = LineStyle.Solid)]
public IndicatorDataSeries tau { get; set; }
[Output("HMA1", LineColor = "WhiteSmoke", LineStyle = LineStyle.Solid)]
public IndicatorDataSeries hma1 { get; set; }
[Output("HMA2", LineColor = "WhiteSmoke", LineStyle = LineStyle.Lines)]
public IndicatorDataSeries hma2 { get; set; }
[Output("TMA", LineColor = "Goldenrod", LineStyle = LineStyle.Solid)]
public IndicatorDataSeries tma { get; set; }
[Output("FCU", LineColor = "LimeGreen", LineStyle = LineStyle.Dots)]
public IndicatorDataSeries fcu { get; set; }
[Output("FCL", LineColor = "DodgerBlue", LineStyle = LineStyle.Dots)]
public IndicatorDataSeries fcl { get; set; }
private TriangularMovingAverage tmaBias;
private HullMovingAverage hma1Bias;
private HullMovingAverage hma2Bias;
private FractalChaosBands fractalBias;
public int ix { get; set; }
private double[,] ai = new double[10, 10];
private double[] b = new double[10];
private double[] x = new double[10];
private double[] sx = new double[10];
private double[] sy = new double[10];
private double sum;
private int ip, ip2;
private int p, p2;
private int n;
private double qq;
private double mm;
private double tt;
private int ii;
private int jj;
private int kk;
private int ll;
private int nn, nn2;
private double sq;
private double sq2;
private double sq3;
private int i0 = 0;
private int mi;
private double t1s1, t1s2, t1roc, t1torsion;
private double t2s1, t2s2, t2roc, t2torsion;
protected override void Initialize()
{
tmaBias = Indicators.TriangularMovingAverage(Source, tmaPeriod);
hma1Bias = Indicators.HullMovingAverage(Source, hma1Period);
hma2Bias = Indicators.HullMovingAverage(Source, hma2Period);
fractalBias = Indicators.FractalChaosBands();
}
public override void Calculate(int index)
{
int i = index;
ix = i;
ip = cog1Period;
ip2 = cog2Period;
p = ip;
p2 = ip2;
sx[1] = p + 1;
sy[1] = p2 + 1;
nn = cog1Degree + 1;
nn2 = cog2Degree + 1;
//COG1
//----------------------sx-------------------------------------------------------------------
//
for (mi = 1; mi <= nn * 2 - 2; mi++)
{
sum = 0;
for (n = i0; n <= i0 + p; n++)
{
sum += Math.Pow(n, mi);
}
sx[mi + 1] = sum;
}
//----------------------syx-----------
for (mi = 1; mi <= nn; mi++)
{
sum = 0.0;
for (n = i0; n <= i0 + p; n++)
{
if (mi == 1)
sum += Source[index - n];
else
sum += Source[index - n] * Math.Pow(n, mi - 1);
}
b[mi] = sum;
}
//===============Matrix=======================================================================================================
for (jj = 1; jj <= nn; jj++)
{
for (ii = 1; ii <= nn; ii++)
{
kk = ii + jj - 1;
ai[ii, jj] = sx[kk];
}
}
//===============Gauss========================================================================================================
for (kk = 1; kk <= nn - 1; kk++)
{
ll = 0;
mm = 0;
for (ii = kk; ii <= nn; ii++)
{
if (Math.Abs(ai[ii, kk]) > mm)
{
mm = Math.Abs(ai[ii, kk]);
ll = ii;
}
}
if (ll == 0)
return;
if (ll != kk)
{
for (jj = 1; jj <= nn; jj++)
{
tt = ai[kk, jj];
ai[kk, jj] = ai[ll, jj];
ai[ll, jj] = tt;
}
tt = b[kk];
b[kk] = b[ll];
b[ll] = tt;
}
for (ii = kk + 1; ii <= nn; ii++)
{
qq = ai[ii, kk] / ai[kk, kk];
for (jj = 1; jj <= nn; jj++)
{
if (jj == kk)
ai[ii, jj] = 0;
else
ai[ii, jj] = ai[ii, jj] - qq * ai[kk, jj];
}
b[ii] = b[ii] - qq * b[kk];
}
}
x[nn] = b[nn] / ai[nn, nn];
for (ii = nn - 1; ii >= 1; ii--)
{
tt = 0;
for (jj = 1; jj <= nn - ii; jj++)
{
tt = tt + ai[ii, ii + jj] * x[ii + jj];
x[ii] = (1 / ai[ii, ii]) * (b[ii] - tt);
}
}
sq = 0.0;
sq2 = 0.0;
sq3 = 0.0;
for (n = i0; n <= i0 + p; n++)
{
sum = 0;
for (kk = 1; kk <= cog1Degree; kk++)
{
sum += x[kk + 1] * Math.Pow(n, kk);
}
cog1[index - n] = (x[1] + sum);
sq += Math.Pow(Source[index - n] - cog1[index - n], 2);
sq2 = sq;
sq3 = sq;
}
sq = Math.Sqrt(sq / (p + 1)) * cogBand1;
sq2 = Math.Sqrt(sq2 / (p + 1)) * cogBand2;
sq3 = Math.Sqrt(sq3 / (p + 1)) * cogBand3;
for (n = 0; n <= cog1Period; n++)
{
c1h1[index - n] = cog1[index - n] + (sq * longScale);
c1h2[index - n] = cog1[index - n] + (sq2 * longScale);
c1h3[index - n] = cog1[index - n] + (sq3 * longScale);
c1l1[index - n] = cog1[index - n] - (sq * shortScale);
c1l2[index - n] = cog1[index - n] - (sq2 * shortScale);
c1l3[index - n] = cog1[index - n] - (sq3 * shortScale);
}
cog1[index - n] = double.NaN;
c1h1[index - n] = double.NaN;
c1h2[index - n] = double.NaN;
c1h3[index - n] = double.NaN;
c1l1[index - n] = double.NaN;
c1l2[index - n] = double.NaN;
c1l3[index - n] = double.NaN;
// COG2
//----------------------sx-------------------------------------------------------------------
//
if (cog2Period > 0 && cog2Degree > 0)
{
for (mi = 1; mi <= nn2 * 2 - 2; mi++)
{
sum = 0;
for (n = i0; n <= i0 + p2; n++)
{
sum += Math.Pow(n, mi);
}
sy[mi + 1] = sum;
}
//----------------------syx-----------
for (mi = 1; mi <= nn2; mi++)
{
sum = 0.0;
for (n = i0; n <= i0 + p2; n++)
{
if (mi == 1)
sum += Source[index - n];
else
sum += Source[index - n] * Math.Pow(n, mi - 1);
}
b[mi] = sum;
}
//===============Matrix=======================================================================================================
for (jj = 1; jj <= nn2; jj++)
{
for (ii = 1; ii <= nn2; ii++)
{
kk = ii + jj - 1;
ai[ii, jj] = sy[kk];
}
}
//===============Gauss========================================================================================================
for (kk = 1; kk <= nn2 - 1; kk++)
{
ll = 0;
mm = 0;
for (ii = kk; ii <= nn2; ii++)
{
if (Math.Abs(ai[ii, kk]) > mm)
{
mm = Math.Abs(ai[ii, kk]);
ll = ii;
}
}
if (ll == 0)
return;
if (ll != kk)
{
for (jj = 1; jj <= nn2; jj++)
{
tt = ai[kk, jj];
ai[kk, jj] = ai[ll, jj];
ai[ll, jj] = tt;
}
tt = b[kk];
b[kk] = b[ll];
b[ll] = tt;
}
for (ii = kk + 1; ii <= nn2; ii++)
{
qq = ai[ii, kk] / ai[kk, kk];
for (jj = 1; jj <= nn2; jj++)
{
if (jj == kk)
ai[ii, jj] = 0;
else
ai[ii, jj] = ai[ii, jj] - qq * ai[kk, jj];
}
b[ii] = b[ii] - qq * b[kk];
}
}
x[nn2] = b[nn2] / ai[nn2, nn2];
for (ii = nn2 - 1; ii >= 1; ii--)
{
tt = 0;
for (jj = 1; jj <= nn2 - ii; jj++)
{
tt = tt + ai[ii, ii + jj] * x[ii + jj];
x[ii] = (1 / ai[ii, ii]) * (b[ii] - tt);
}
}
for (n = i0; n <= i0 + p2; n++)
{
sum = 0;
for (kk = 1; kk <= cog2Degree; kk++)
{
sum += x[kk + 1] * Math.Pow(n, kk);
}
cog2[index - n] = (x[1] + sum);
}
cog2[index - cog2Period] = double.NaN;
}
// TORSION
if (torsionPeriod > 0 && cog1Degree > 1)
{
for (n = i0; n <= i0 + torsionPeriod; n++)
{
t1s1 = (cog1[index - 1] - cog1[index - torsionPeriod - 1]);
t1s2 = (cog1[index] - cog1[index - torsionPeriod]);
t1roc = (t1s2 - t1s1);
t1torsion = (t1s2 + t1roc);
if (cog2Degree > 1 && cog2Period > 0)
{
t2s1 = (cog2[index - 1] - cog2[index - torsionPeriod - 1]);
t2s2 = (cog2[index] - cog2[index - torsionPeriod]);
t2roc = (t2s2 - t2s1);
t2torsion = (t2s2 + t2roc);
}
else
t2torsion = 0;
tau[index - n] = t1torsion + t2torsion + Source[index - n];
}
tau[index - cog1Period] = double.NaN;
}
if (tmaPeriod > 0)
{
for (n = i0; n <= i0 + tmaPeriod; n++)
{
tma[index - n] = tmaBias.Result[index - n];
}
tma[index - cog1Period] = double.NaN;
}
if (hma1Period > 0)
{
for (n = i0; n <= i0 + hma1Period; n++)
{
hma1[index - n] = hma1Bias.Result[index - n];
}
hma1[index - cog1Period] = double.NaN;
}
if (hma2Period > 0)
{
for (n = i0; n <= i0 + hma2Period; n++)
{
hma2[index - n] = hma2Bias.Result[index - n];
}
hma2[index - cog1Period] = double.NaN;
}
if (fractalFilter)
{
for (n = i0; n <= i0 + cog1Period; n++)
{
fcu[index - n] = fractalBias.High[index - n];
fcl[index - n] = fractalBias.Low[index - n];
}
fractalBias.High[index - cog1Period] = double.NaN;
fractalBias.Low[index - cog1Period] = double.NaN;
}
}
}
}
nobulart
Joined on 03.09.2013
- Distribution: Free
- Language: C#
- Trading platform: cTrader Automate
- File name: Aurea Draconis Torsion 4.3.algo
- Rating: 5
- Installs: 1760
- Modified: 13/10/2021 09:54
Note that publishing copyrighted material is strictly prohibited. If you believe there is copyrighted material in this section, please use the Copyright Infringement Notification form to submit a claim.
Comments
Log in to add a comment.
No comments found.